GUINIER ANALYSIS¶
アンドレ・ギニエから名付けられたギニエ解析は、非常に小さな散乱角でのSAXS散乱曲線の解析を指す。この分析はSAXSのinvariants、回転半径 Rg 、ゼロ散乱角 l(0) における外挿強度の直接推定が可能である。 Rg を決定する際に、ScAtterと古いPrimusバージョンを示す。
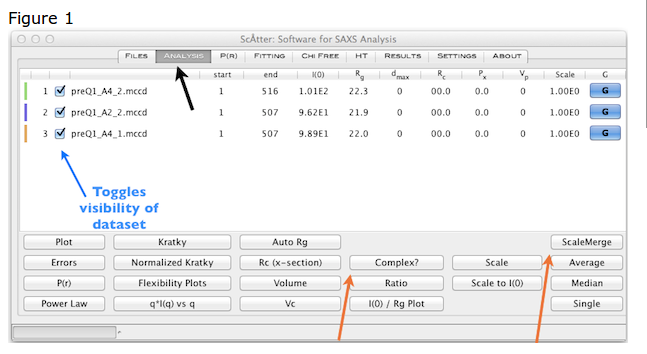
ファイルを読み込んだ後、 をクリックする(図1の黒い矢印)。
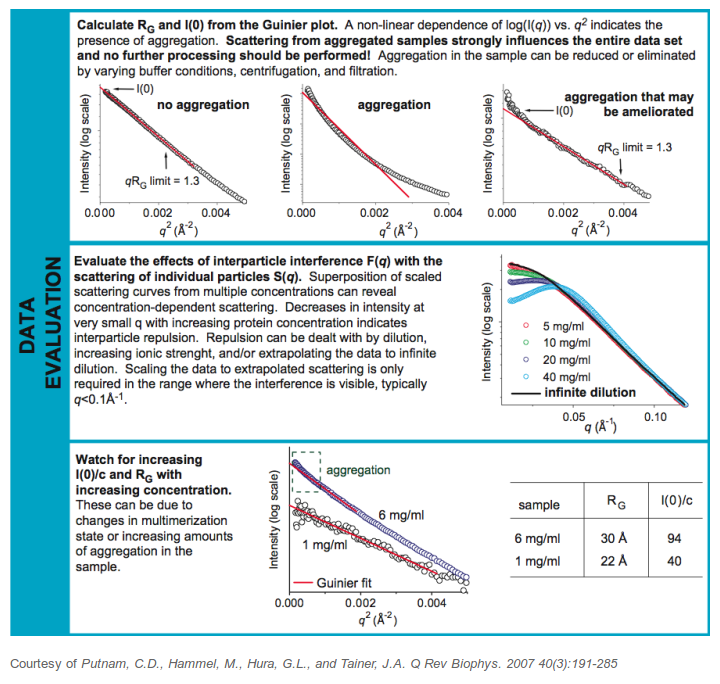
Rg を決定する方法には、自動化方法と手動方法がある。自動化された方法( Auto Rg )は \(q \times Rg <1.3\) ( Svergun and Feign1982の71ページ参照)によって制限された小角 q 領域のデータ内の最良フィットを決定する。この方法では、曲線から不良点を取り除くことはできませんが、フィットの生成されたプロットは、粒子間の干渉や凝集によって、データが破損する可能性のある箇所を確認するのに役立つ。
手動のギニエ解析の場合は、青色(右側)で強調表示された” “ボタンを押す。
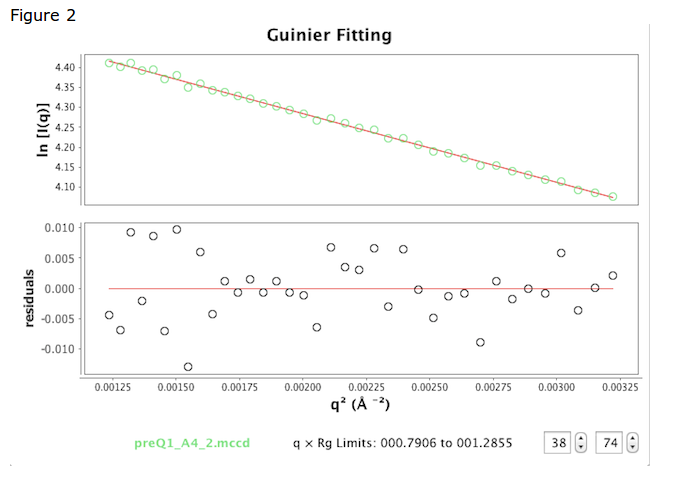
ギニエ領域で、初期の最良フィットを示すプロットが表示される。上側のプロットはデータとフィットで、 \(\ln [I(q)]\) 対 \(q^2\) 下側のプロットで対応する残渣である。ギニエのパラメーターは で更新され、視点の数は と ボックスで自動的に更新される(図2の右下)。ポイントを手動で追加または削除するには、番号横にある矢印を使用する。
目標は、データの小角 q 領域の開始点から非線形点を削除することである。残渣の曲線は非線形性を示唆している。最大 q 値は、 ボックスで指定した \(q \times Rg <1.3\) (黄色の円図2)に制限する必要がある。なぜ1.3なのだろうか。FeigunとSvergunのSAXSの本から、不等式は、推定されたパラメーターが真の値の10%以内であることを保証する。ギニエ解析は、SAXS曲線の近似であることを忘れないでほしい。したがって、これらのパラメーター l(0) また Rg は、どれだけのデータ点数がギニエ近似に使われるか、あるいは同様にデータの質に依存して誤差を伝播されやすい。
ギニエのパラメーターは で継続的に更新される。現在表示されている値は、 に保存されている値である。
ギニエ領域の精査は定性的に予期しない試料のふるまいを明らかにし、試料凝集または濃度依存散乱の存在を評価するのに有用である。これはギニエ領域の非線形性に代表される。詳細は、Putnam, C.Dなどをみてほしい。
PRIMUS (WINDOWS ONLY)¶
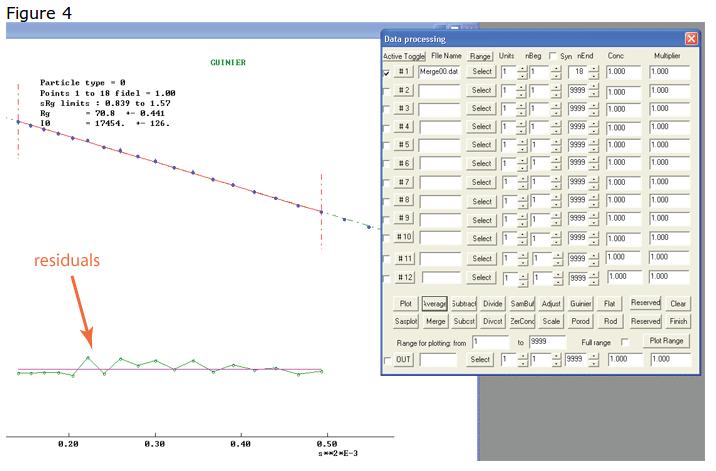
プリマスのために、マージされたデータを開けてもらいたい。前のデータを削除するには、 の右下隅にある ボタンをクリックする。対象のデータを選択し、 ボタンを押してから ボタンを押す。曲線は図3のように大きく違っているように見えるはずである。赤く円で囲まれている sRg または qRg 限界は9.29であり、それははるかに大きく、1.3未満でなければならない。だから、 nEnd を調節して、エンドポイントの数を減らさなければならない。502 と表示されているところに50を入力し、もう一度 ボタンを押すことによってできる。
再プロットしたデータは、選択された q 範囲内ではるかに線形に見えるはずである。図4に示すデータは、非常に大きな巨大分子である30Sリボソームサブユニットに由来し、ギニエ領域は約18ポイントを含む。ほとんどの場合、より小さな巨大分子(1,000kDa未満)では、ギニエ領域ではさらに多くの有用な点があり、12,000eVで100kDa付近のものは、約30ポイントになる。
図4の一番下の行には、線形近似の残渣が表示される。残渣を偏らせるように見えるポイントを減らしている間、 sRg 制限が小球状粒子(タンパク質)のために1.3未満になるように、 と を調節するべきである。図4のフィットは、 Rg が70.8、 l(0) が17,454で合理的である。 Rg がより小さな散乱角でより多くのデータを必要とするなら、エネルギーを12,000eVから8,000eVに下げる必要がある。
よいふるまいを示す試料の場合、測定強度の自然対数のプロット対 \(q^2\) はデータの最小 q 領域に線形領域を示すはずである。切片 b はゼロ角度で外挿された強度であり、傾き m は Rg の負の2乗を3で割ったものである。